Tesseracts, a brief geometric excursion
Tesseracts, a brief geometry
A tesseract is a four-dimensional shape analogous to a cube. That is, in two dimensions we have a square, in three dimensions a cube, and in four dimensions a tesseract (or hypercube). Just as a cube has surfaces that are squares, a tesseract has surfaces that are cubes. While probably nobody can directly visualize a tesseract, we can look at models of a tesseract in three dimensions—just as we can look at pictures of a cube in two dimensions.
At the top of Figure A, a model of a tesseract is shown. It appears as a little cube inside a big cube, with each corner of the little cube attached to the nearest corner of the big cube. (For clarity, the ratio of sizes of the two cubes has been made large; a more literally correct tesseract model would show the two cubes as differing only slightly in size.)
Figure A. Cubes and Tesseracts
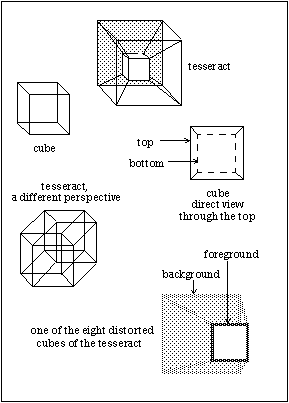
This model, which seems to be made up of only two connected cubes, actually contains eight cubes. Due to perspective, not all of these are immediately recognizable as cubes. Consider just the shaded back face of the large cube, the back face of the little cube, and the lines connecting them. This composite object, drawn from a somewhat different perspective, is shown at the lower right. It's shaped like a chopped pyramid (the “frustrum” of a pyramid). The apparent frustrum is really a cube distorted in perspective—a side effect of projecting a four-dimensional object into three dimensions.
There are six objects of the frustrum-type in the tesseract model. But the projection that causes these distortions in shape also causes distortions in size. For instance, the “big” outer cube and “small” inner cube are the same size in four dimensions. All eight of the tesseract's cubes are identical in size and shape in the four-dimensional original.
Three-dimensional objects viewed in two dimensions go through similar distortions of perspective. As the diagram of the cube near the left edge of Figure A shows, the six identical squares that make up a cube appear as two squares and four lopsided parallelograms.
If you look down through the top of a glass cube (see the diagram), the base of the cube seems to be a small square inside the larger square at the top. But this is perspective again. Both squares are identical. Of course, this view of the cube is directly analogous to the tesseract seen as a small cube inside a larger one.
Tesseracts can also be presented in different perspectives, as is shown by the tesseract at the left of Figure A, where the distortions assume a different and more intricate form. This is analogous to the cube shown at the left of the figure
It is useful, in visualizing a tesseract, to unfold one—“flattening” it into three dimensions. The unfolding process for tesseracts is similar to the unfolding of a cube.
When a cube (such as a cardboard box) is unfolded, there is a side attached to each edge of the base square—then, one extra square (the top of the box) extending from one end, as in Figure B.
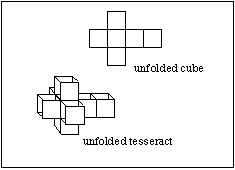
When a tesseract is unfolded into three dimensions, you get a central cube with another cube attached to each face—and an extra cube extending from one end of the structure.
The way in which the name Glass Tesseract became the name of this magazine is another story. In the search for a name, it became clear that many good one-word names were already taken. Furthermore, it wasn't obvious how to ascertain that a particular word was not being used by someone, even when it wasn't found. The obvious solution was to start putting together two-word combinations that didn't sound very common. In this process of free association, “Glass Tesseract” floated to the surface.
Despite its origins in a chaotic process, the name was immediately appealing. “Tesseract” suggests dimensionality—multiple dimensions of meaning or feeling within a single story or poem—or the dimensionality implicit in a diverse body of contrasting works.
“Glass” evokes the ability to see into this dimensionality, either through a clear and transparent medium—or else through a clouded translucence (as in the well-known quotation from Paul *), wherein all aspects are not immediately visible.
And so, Glass Tesseract it became.
Michael Chester
* I Corinthians 13:12